El procesamiento digital de
imágenes es el conjunto de técnicas que se aplican a las imágenes digitales
con el objetivo de mejorar la calidad o facilitar la búsqueda de información.
La
edición digital de imágenes se ocupa de
la edición apoyada en computadores de imágenes digitales, comúnmente un
gráfico rasterizado, en la mayoría de los casos
fotos o documentos
escaneados. Estas imágenes son editadas
para optimizarlas, manipularlas, retocarlas, etc con el fin de alcanzar la meta
deseada.
Una de las metas puede ser eliminar las fallas
que pueden haberse producido durante el escanéo o al fotografiar, por ejemplo
sobreexposición,
baja exposición, falta de
contraste,
ruido
en la imagen,
efecto de los ojos rojos, paradoja de las
líneas paralelas en perspectiva, etc. Estas fallas se producen por defectos
técnicos en los aparatos fotográficos, escáner, condiciones de trabajo
precarias, fallas en la operación u originales defectuosos.
Las imágenes al lado derecho muestran algunas de
las potencialidades de la edición de imágenes: la imagen superior se ve oscura,
el texto difuso y el motivo fuera de centro. La imagen inferior está corregida
y se ve más nítida, mejor iluminada y el objeto, puesto más al centro, se ve
más presente.
El retoque tradicional es reemplazado cada vez
más por la edición digital, a menudo la edición de imágenes digitales está
incluida dentro del proceso de impresión digital.
Algunas funciones de
la edición digital de imágenes
Efectos gráficos.
Ejemplo de rotación de
imágenes.
Ejemplo de cambio de
color.
Imagen original.
Las ramas de la imagen
original fueron retiradas con un timbre.
Original en color.
Resaltar una sección
por medio de colores.
Imagen original.
Retoque con
Fotostudio, luz, contraste, nitidez.
La catedral de Reims
con perspectiva.
La catedral de Reims
con corrección de perspectiva.
A la
aplicación con la cual se
realiza la edición digital de imágenes se le llama
editor de imágenes,
el cual ofrece numerosas funciones en un menú o en una ventana de herramientas.
Algunas de estas funciones son:
- Oscurecer y aclarar: Por medio de estos algoritmos digitales se
pueden imitar los logros de una virtual prolongación o disminución del tiempo
de exposición de una virtual foto.
- Selección: Algunas secciones de la imagen pueden ser seleccionadas por medio de
círculos, rectángulos, lazos, polígonos, rangos de coloraciones, etc. Cada
selección puede ser la inicial, agregarse a la ya existente o sustraerse
de la ya existente. Después la selección puede ser tratada en forma aparte
del resto de la imagen.
- Correcciones automáticas: Para neófitos, algunos editores de imágenes
ofrecen procedimientos automáticos de corrección. Estos modifican
automáticamente el color, el tono, el contraste y otros factores de la
imagen sin intervención del principiante. Sus resultados pueden no
satisfacer a un profesional.
- Colorkey: La técnica colorkey realza algún motivo de la imagen dándole color en un tranfondo de
tonos grises
- Almacenar: Este nombre genérico incluye por lo menos tres posibilidades:
- Almacenar la imagen en el formato actual,
- Convertir el formato actual
a algún otro y luego almacenar la imagen en ese nuevo formato o
- Almacenar en el formato actual
pero bajo un nuevo nombre.
- Rotar: Por medio de la rotación de una imagen pueden ser corregidas leves
fallas al hacer la imagen, ya sea al fotografiar, escanear ó al crearla
por medio del editor de imágenes. También pueden ser logrados algunos
efectos deseados en la imagen.
- Planos: Planos son folios virtuales que contienen algunos elementos de la
imagen que el usuario desea mantener separados del resto. Estos elementos
se pueden estar distribuidos por sobre toda la imagen. Planos pueden ser
marcados visibles o invisibles, pueden ser antepuestos o postergados en
relación a otros planos. Ver Técnica de planos.
- Informaciones EXIF: Muestra las eventuales informaciones Exif
incluidas en el archivo. Estas pueden ser en el caso de fotos: fecha de
creación, abertura del diafragma, tiempo de exposición, fabricante de la
máquina fotográfica, etc. Ver IPTC, Metadato.
- Color: El color juega en
la edición de imágenes un rol importante. Las cualidades del color de la
imagen pueden ser cambiadas con estas herramientas, como el tono, el
matiz, valor o luminosidad, contraste simultáneo, la saturación, el modelo
de color (RGB, CMYK, HSV)1
- Modelo de color y profundidad del color: Una
imagen puede ser llevada al modelo de color deseado y posible: Bitmap,
tonos grises, colores indexados, duplex, RGB, Lab y CMYK. Según el modelo
de color se obtiene una diferente profundidad
de color. Se distingue según la profundidad de color entre color verdadero, Color de
alta resolución, color
indexado, pero también entre tonos gises y blancoynegro.
- Filtro: Las imágenes pueden ser modificadas por medio de filtros. Estos
pueden dar a la imagen un aspecto más amarillento par envejecer la imagen,
más brillante, pueden crear un relieve sobre la imagen o hacer aparecer
una fuente de luz o disminuor la nitidez de la imagen. Ver Filtros para imágenes y Plugin.
- Efectos: Se le puede dar a la imagen un efecto especial, como movimiento,
vista tras un vidrio con gotas de lluvia, tipo mosaico, etc.
- Fotomontaje: En el Fotomontaje varias
imágenes son añadidas en una especie de composición. Ver también Collage.
- Fotomosaico: En el Foto
mosaico la imagen general o mayor está compuesta de muchas imágenes más
pequeñas y una visión rápida muestra el tema o figura mayor, pero una
visión más detallada muestra que cada uno de las imágenes que forma la
imagen mayor, es a su vez una imagen particular. Ver Collage.
- Retirar: Regiones innecesarias de una imagen son retiradas para utilizar solo
los objetos con que se quiere trabajar o resaltar. Es decir es un proceso
que es posterior a la Selección y anterior al Collage, Fotomontaje u otros.
- Inundar: La herramienta inundar sirve para llenar de un color elegible toda
una región que debe estar delimitada completamente.
- Corrección gamma: Con la herramienta corrección
gamma se modifican la luminosidad y los tonos.
- Histograma: Con un Histograma de una imagen se pueden
corregir fallas en la distribución de los colores de la imagen. Es muy
importante en la corrección de fallas en los tonos.
- Invertir: Con la inversión del
color se cambia el color de un píxel por el
opuesto en el modelo
de color RGB substrayendo para cada color, R, G, B, el valor del color del máximo
(255).
- Canales: Un Canal de
color significa que cada color primario utiliza
un canal. En CMYK hay
cuatro canales, cian, magenta, amarillo y negro, y en RGB tres
canales: rojo, verde y azul. Además existen canales alfa en que se almacenan selecciones y máscaras.
- Corrección perspectiva: Con giro se pueden corregir fallas en la
perspectiva de una imagen. Ver Corrección perspectiva.
- Colorear: La herramienta colorear permite dar:
- A toda la imagen un color en diferentes tonos.
- A alguna región de la imagen un color.
- Quitar o disminuir la intensidad de un color en una región de la
imagen.
- Convertir: Permite convertir el archivo de un formato a otro.
- Timbre: Sirve para copiar secciones de la imagen a otros lugares de la imagen
con el fin de corregir errores o encubrir objetos no deseados en la
imagen.
- Lazo: Con el lazo el usuario puede seleccionar una región con una línea
trazada a pulso.
- Macros: Es una secuencia de comandos de elaboración con el fin de obtener un
efecto, que se almacena y que puede entonces ser aplicada cuantas veces
sea necesaria, también en otras imágenes.
- Pintar: Una de las funciones más básicas de un editor de imágenes es la función
pintar. Para ello se pueden utilizar diferentes herramientas como lápiz,
spray, etc., (Ver Lápiz (herramienta)) para simular diferentes técnicas de pintura. Se
debe diferenciar "pintar" de "dibujar"; Al pintar se
cambian las características de cada pixel, uno por uno. Al dibujar se
definen lugares geométricos por medio de definiciones matemáticas (vectores
o senderos) como círculos, elipses, curvas, etc. Más tarde esas figuras
geométricas son convertidas en pixel, pero hasta entonces son objetos
geométricos.
- Enmascarar: Al enmascarar se selecciona determinadas regiones de la imagen para
sustraerlas de la elaboración que viene. Se puede ampliar con un pincel o
reducir con el borrador. De esta manera se puede trabajar sin dañar otras
regiones.
- Monocolor: En este modo se crean imágenes de un solo
color pero con diferentes tonos.
- Panorama: A partir de imágenes sectoriales se puede crear una imagen
panorámica uniendo las sectoriales y, si es necesario, sobreponiéndolas en las
regiones visuales que se repiten. Para ello se puede utilizar stichting software.
- Dibujar: Con vectores o senderos se pueden dibujar elementos geométricos
sencillos. Para dibujar vectores más complejos debe usarse un programa
para Scalable Vector Graphics.
- Pipeta: La pipeta sirve para captar desde la imagen el color de un pixel
determinado para copiarlo en otras regiones.
- Borrador: Con él se eliminan las informaciones guardadas en un pixel
determinado. Sus propiedades, tamaño y transparencia, pueden ajustarse a
las necesidades.
- Nitidez: Reducir o aumentar la nitidez de la imagen para por ejemplo esconder
algún trasfondo indeseado.
- Escalar: La cantidad de pixels que tiene una imagen se puede variar. La
variación del largo y el ancho puede ser proporcional conservando las
proporciones de la imagen ó en caso contrario se distorsiona la imagen. Al
escalar, la imagen continúa ocupando la misma proporción de la tela que
antes.
- Ampliar: También se puede variar las dimensiones de la tela en que está la
imagen, sin modificar la imagen, creando un nuevo espacio vacío para
nuevos motivos ó recortando la imagen al reducir la tela.
- Solarización: Al solarizar se invierte el color
de los píxeles cuya luminosidad sobrepase un límite.
- Reflejar: Reflejar la imagen (verticalmente u horizontalmente) significa
reflejarla en un espejo virtual vertical u horizontal y sirve para
corregir documentos escaneados en la posición equivocada.
- Procesamiento por lotes: Scripts o macros
son ejecutados sobre una pila de archivos (imágenes) automáticamente. Son
muy útiles para el trabajo con álbumes.
- Texto: Permite escribir texto sobre la imagen, con elección de tipo, tamaño,
color, dirección de la escritura, etc.
- Amplitud de tono: La amplitud de tono es la diferencia entre el pixel más obscuro y el
pixel más claro de un color en el modelo
de color RGB. La amplitud de tono ideal es un buen balance entre obscuridad y luz
en los colores. El histograma sirve para diagnosticar las fallas. Se puede
mejorar las fallas regulando la saturación, la
luminosidad y el contraste.
- Compresión: Al almacenar un archivo el programa ofrece elegir el grado de
compresión del archivo o la resolución de la
imagen. Esto influye sobre el volumen del archivo y así sobre la rapidez
de su transmisión en internet.
- Gradiente: Sobre una superficie esta herramienta permite cambiar de un color a
otro continuamente a lo largo de un eje de avance. Por ejemplo, se puede
simular un juego de luz y sombra en un cilindro iluminado. Ver Gradiente (gráfica).
- Varita mágica: Herramienta para seleccionar todos los píxeles que tengan un color
dentro de un rango determinado.
- Zoom: Para muchos trabajos a realizar es necesario una visión más detallada
de la región, por ejemplo para corregir errores. Esto se obtiene con la
herramienta zoom que aumenta o disminuye el acercamiento virtual de la
imagen.
Las imágenes modificadas por el editor de imágenes
digitales se utilizan posteriormente en publicaciones: revistas, catálogos,
libros y otros medios impresos y electrónicos. Rostros sin arrugas, piel
inmaculada, paisajes perfectos y otras características son una consecuencia de
la elaboración digital, lo cual borra cada día más las fronteras de la
realidad. Por ello, la edición de imágenes digitales se puede utilizar
intencionalmente para la manipulación de imágenes. Sin embargo, no podemos
dejar sin considerar el factor Arte. La edición de imágenes es una posibilidad
de desarrollo artístico y así es considerada actualmente en el Arte digital y
Multimedia.
Campos de acción de la
edición de imágenes:
La edición digital de imágenes se expande cada día
más, porque la
fotografía
digital puede transferir sus fotos directamente a la computadora. En el campo de
acción casero existen programas editores de imágenes especialmente diseñados
para el uso en casa, ofreciendo, entre otros, correcciones automáticas.
En el campo profesional, la edición de imágenes
digitales es utilizada por fotógrafos, diseñadores en
autoedición y en la
preimpresión.
Las imágenes modificadas por el editor de imágenes
digitales se utilizan posteriormente en publicaciones: revistas, catálogos,
libros y otros medios impresos y electrónicos. Rostros sin arrugas, piel
inmaculada, paisajes perfectos y otras características son una consecuencia de
la elaboración digital, lo cual borra cada día más las fronteras de la
realidad. Por ello, la edición de imágenes digitales se puede utilizar
intencionalmente para la manipulación de imágenes. Sin embargo, no podemos
dejar sin considerar el factor
Arte. La edición de imágenes es una posibilidad de desarrollo artístico y así
es considerada actualmente en el
Arte digital y
Multimedia.
Qué es una
interfaz gráfica de usuario
|
La
interfaz gráfica de usuario, conocida
también como
GUI (del
inglés graphical user
interface) es un
programa
informático que actúa de
interfaz de
usuario, utilizando un conjunto de imágenes y
objetos gráficos para representar la información y acciones disponibles en la interfaz. Su
principal uso, consiste en proporcionar un entorno visual sencillo para
permitir la comunicación con el
sistema operativo de una máquina o
computador.
Habitualmente las acciones se realizan mediante
manipulación directa, para facilitar la interacción del usuario con la
computadora. Surge como evolución de las interfaces de
línea de
comandos que se usaban para operar los primeros
sistemas operativos y es pieza
fundamental en un
entorno
gráfico. Como ejemplos de interfaz gráfica de usuario, cabe citar los entornos de
escritorio
Windows, el
X-Window de
GNU/Linux o el de
Mac OS X,
Aqua.
En el contexto del proceso de interacción
persona-
ordenador, la interfaz gráfica
de usuario es el artefacto tecnológico de un sistema interactivo que
posibilita, a través del uso y la representación del
lenguaje visual, una interacción
amigable con un sistema
informático.
Tipos de
interfaces gráficas de usuario
GUI's y Zooming user
interface:
Los tipos de GUIs que se encuentran en juegos de computadora, y
los GUIs avanzados basados en realidad virtual, se usan con frecuencia en
tareas de investigación. Muchos grupos de investigación en Norteamérica y
Europa están trabajando actualmente en la interfaz de enfoque del usuario
o ZUI (Zooming User Interface), que es un adelanto lógico de las GUI,
mezclando 3D con 2D. Podría expresarse como "2 dimensiones y media en
objetos vectoriales de una dimensión".
Interfaz
de usuario de pantalla táctil:
Algunos GUIs son diseñados para cumplir con los rigurosos
requisitos de los mercados verticales. Éstos se conocen como "GUIs de uso
específico." Un ejemplo de un GUI de uso específico es la ahora familiar touchscreen o
pantalla táctil (pantalla que al ser tocada efectúa los comandos del ratón
en el software). Se encuentra actualmente implementado en muchos restaurantes y
en muchas tiendas de autoservicio de todo el mundo. Fue iniciado por Gene Mosher en la computadora del ST de Atari
en 1986,
el uso que él específico en las GUIs de pantalla táctil ha encabezado una
revolución mundial en el uso de las computadoras a través de las industrias
alimenticias y de bebidas, y en ventas al por menor.
Otros ejemplos de GUIs de uso específico, relacionados con la
pantalla táctil son los cajeros automáticos, los kioscos de información y las
pantallas de monitoreo y control en los usos industriales, que emplean un sistema operativo de tiempo real
(RTOS). Los teléfonos
móviles y los sistemas o consolas de juego también emplean las pantallas
táctiles. Además la domótica
no es posible sin una buena interfaz de usuario, o GUI.
Interfaz
Natural de Usuario:
Las NUI
naturales son aquellas en las que se interactúa con un sistema, aplicación,
etc., sin utilizar dispositivos de entrada como ratón, teclado, lápiz óptico,
etc. En lugar de éstos se utilizan las manos o las yemas de los dedos.
Formatos
Gráficos de Almacenamiento
|
Formatos
de archivos gráficos más conocidos:
Un formato de archivo gráfico es el modelo que se usa para almacenar la
información de una imagen en un archivo. Para usar una imagen en un programa de
aplicación, éste debe reconocer la estructura del archivo donde se encuentra
almacenada la imagen, es decir, la aplicación debe soportar el formato del
archivo.
-(.bmp): (Windows Bitmap) Comúnmente usado por los programas de Microsoft
Windows y por el sistema operativo propiamente dicho.
(.psd): (Photoshop Document) Formato nativo de Adobe Photoshop, Permite el
almacenamiento de múltiples capas, cada una de las cuales puede contener una
imagen del tipo bitmap o vectorial.
-(.xpm): (X-Pixmap)
Es un formato gráfico, en ASCII y formato en C (parece un archivo en C).
-(.jpeg): (Joint Photographic Experts Group) Formato
creado por el comité del mismo nombre que permite la compresión de imágenes
fotográficas a una gran profundidad de colores (millones de ellos).
-(.cdr): (CorelDRAW)Formato vectorial para
aplicaciones CorelDRAW.
-(.pdf): (Portable
Document Format) En esencia no es un formato gráfico propiamente dicho, sino un
formato de almacenamiento de documentos, que permite almacenar texto con
formato, imágenes de diferentes tipos, etc. Es una versión simplificada de
PostScript; permite contener múltiples páginas y enlaces.
-(.gif): (Graphics Interchange Format) Es un
formato gráfico utilizado ampliamente en la World Wide Web, tanto para imágenes
como para animaciones. Tiene un formato de 8 bits (256 colores máximo), con
soporte de animación por cuadros
Hardware y Software disponibles para la graficación
|
En el campo de la informática gráfica se pueden encontrar diferentes
dispositivos de salida; desde los que permiten obtener representaciones en
soporte físico (impresoras, p.e.) hasta sofisticados sistemas de
"inmersión" capaces de generar todo un entorno de realidad virtual
alrededor del usuario.
Por el momento nos concentraremos en los dispositivos de salida a
vídeo, por ser los mas comunes y por constituir la base de otros muchos
sistemas de visualización.
La tecnología en la que aún están basados la mayor parte de los
monitores es el tubo de rayos catódicos (CRT); aunque parece estar siendo
desplazada por la tecnología de cuarzo líquido (LCD).
Un CRT básicamente consiste en un tubo de vacío en cuyo interior un
cátodo de metal calentado mediante un filamento por el que circula corriente
eléctrica. El calor propicia el desprendimiento de electrones del cátodo; estos
electrones, cargados negativamente, atraviesan diferentes dispositivos de
enfoque y aceleración, y mediante los adecuados sistemas de control de
deflexión son dirigidos a diferentes puntos del otro externo del tubo. En este
extremo se encuentra la pantalla, recubierta internamente de fósforo, fósforo
que al recibir el impacto de los electrones absorbe su energía, transformándola
parcialmente en calor y utilizando el resto para elevar sus propios electrones
a niveles superiores de excitación. Poco tiempo después estos electrones "excitados"
vuelven a su estado original, desprendiendo el exceso de energía en forma de
fotones; que es lo que produce el punto de la imagen visible.
Así pues, este punto de luz desaparece en el momento en que el fósforo
vuelve a su estado de reposo; el tiempo en que esto tarda en ocurrir define una
de las propiedades mas importantes para diferenciar entre dos fósforos: la
persistencia, que se define como el tiempo que tarda en disminuir la luz
emitida por la pantalla a un décimo de su intensidad inicial. Valores típicos
son de 10 a 60 microsegundos.
Por lo tanto, si deseamos mantener una imagen visible en el CRT
deberemos re-generarla a una velocidad superior a la que tarda en desaparecer
de la pantalla. Los fósforos de menor persistencia serán mas adecuados para
animación; mientras que para mostrar imágenes estáticas puede ser suficiente un
monitor más "lento".
Otra propiedad importante de los tubos es su resolución, generalmente
definida simplemente como el máximo número de puntos luminosos que se pueden
diferenciar. Dado que la luminosidad de un punto decae desde el centro hacia su
periferia, se considera que dos puntos son diferentes cuando su separación es
mayor del diámetro en el que el punto tiene aproximadamente el 60% de la
luminosidad del centro del mismo. Es fácil encontrar monitores que soportan
hasta 1280x1024; a partir de esta resolución se suele hablar de sistemas de
alta definición.
También caracteriza a un tubo su "relación de aspecto", o
relación entre la resolución horizontal y la vertical. La mas frecuente es de
4:3, aunque empiezan a aparecer relaciones "panorámicas" o 16:9, más
apropiadas p.e. para cine en alta definición.
Monitores de barrido:
En el tipo de monitor con CRT más utilizado el haz de electrones
recorre la punto por punto en dirección longitudinal y línea por línea en
dirección vertical, variando su intensidad en cada punto de acuerdo con la
luminosidad correspondiente al punto de la imagen correspondiente que se
pretende representar. La intensidad de cada uno de estos puntos de imagen,
conocidos como "pixels", debe estar almacenada en la memoria del
ordenador (a la memoria encargada de contener esta información se le denomina
búfer de pantalla o frame buffer); si p.e. para representar la intensidad de un
pixel se utilizan 24 bits, para una pantalla de 1024 x 1024 se necesitan 3 Mb
de memoria.
La velocidad a que se realiza este barrido (evidentemente, relacionada
con la persistencia del fósforo) suele darse como característica del monitor;
tanto en la forma de frecuencia de barrido vertical (para toda la imagen), que
suele oscilar entre los 50 y los 80 Hz y la frecuencia de barrido horizontal
(para cada línea) que suele ser del orden de los 40 KHz. Por lo general, una
frecuencia más alta, por lo general, es conveniente para disminuir la fatiga
visual, y necesaria cuando se desea generar imágenes a gran velocidad (p.e.
pares de imágenes estereoscópicas en tiempo real a velocidades de refresco
tales que el ojo no distinga "parpadeos").
En algunos monitores realiza el barrido vertical en dos fases, en la
primera se recorren las líneas impares, y en la segunda las pares. De esta
forma se consigue una frecuencia aparente doble de la real (aparente en el
sentido de que cada imagen se genera en la mitad de tiempo, aunque,
evidentemente la imagen contenga la mitad de la información de la real). Este
sistema se utiliza en los televisores domésticos, lo que puede aprovecharse
también para conseguir una mayor suavidad en las animaciones generadas por
ordenador: Efectivamente, en lugar de generar una imagen cada p.e. 1/60
segundo, se genera la mitad de la imagen cada 1/120 segundo, con lo que el
tiempo de cálculo es el mismo y el movimiento más continuo.
Monitores de trazado
aleatorio o vectoriales:
En este sistema, actualmente menos utilizado, el haz de electrones en
lugar de recorrer la pantalla a base de pixels, traza una serie de segmentos
correspondientes a las líneas de la imagen que se pretende representar.
Así, la imagen está definida en memoria como una sucesión de
instrucciones de trazado y movimiento aleatorio; y esta serie de instrucciones
son ejecutadas por el haz de electrones un mínimo de 30 veces por segundo. Los
sistemas vectoriales de alta calidad pueden llegar a manejar imágenes con
100.000 líneas; cuando la imagen tiene muy pocas líneas se introduce un retraso
entre redibujados, ya que de otra forma se podría llegar a quemar el fósforo.
Monitores CRT en color:
Los monitores CRT en color utilizan una combinación de fósforos que
emiten luz con colores distintos, colores básicos que combinados producen la
sensación de los colores del espectro que se deseen.
Estos monitores utilizan principalmente la técnica de la "máscara
de sombra". Partiendo de un tubo con tres fósforos que emiten, para cada
punto, luz roja, verde y azul, y con tres cañones de electrones, los tres haces
de electrones se enfocan y se hacen coincidir sobre la máscara, que contiene
una serie de orificios alineados con los patrones de punto de fósforo. Cuando
los tres haces pasan por un orificio activan el triángulo correspondiente, que
se ve como un punto de color.
La intensidad de cada haz se controla independientemente, y por lo
general se considera que con una resolución de 8 bits para cada uno (24 en
total, por lo tanto), es decir, 256 niveles de voltaje por cañón para un total
de 256 al cubo (16 Millones) de colores, se obtiene "color real"
(haciendo referencia a la incapacidad del ojo humano de distinguir diferencias
al aumentar la cantidad de niveles por componente).
Monitores de cuarzo
líquido (LCD):
Los monitores de cuarzo líquido utilizan dos placas de cristal que
contienen cada una un polarizador de luz girado 90 grados una respecto a la
otra. Estas placas prensan el cuarzo líquido (con estructura cristalina, pero
con moléculas capaces de fluir como en estado líquido). En una de las placas se
crean líneas verticales de conductores transparentes, y en la otra,
horizontales. La intersección de las líneas define los pixels, de forma que
cuando existe voltaje ambos conductores en ambos conductores las moléculas se alinean
y la luz que atraviesa el cristal no gira y por lo tanto no atraviesa el
segundo cristal.
Cuando la luz se genera mediante un transistor en cada pixel, se habla
de pantallas LCD de matriz activa, siendo esta la tecnología más utilizada en
la actualidad.
Aparte de eso, la representación de la información es similar a la de
los monitores CRT de barrido: también se utiliza el búfer de pantalla con la
imagen formada por pixels.
Graficacion en 2D:
Graficacion en 3D:




QUE ES LA REPRESENTACION BIDIMENSIONAL:
Espacio bi-dimensional es un módulo geométrico de la proyección plana y física del universo donde vivimos. Tiene dos dimensiones, por ejemplo, ancho y largo, pero no profundidad (que solo se utiliza en la tridimensionalidad). Los planos son bidimensionales, y sólo pueden contener cuerpos unidimensionales o bidimensionales.
Toda imagen bidimensional está plasmada sobre algún tipo de soporte. El soporte delimita una "porción de espacio" sobre el que la imagen se extiende y a la vez es sustento de la materia con la que la imagen está realizada.
En su doble condición de espacio de la representación y sostén de la materia, representación, materia y soporte quedan imbricados uno con el otro, formando esa unidad resultante que es la imagen.
Todo tipo de soportes han sido utilizados por el hombre, a través del tiempo, para plasmar sus representaciones. En tanto espacio para la representación encontramos soportes de formatos y dimensiones muy diversos, elegidos en función de la imagen que sobre él se ha realizado.
Éstos son algunos ejemplos de imágenes bidimensionales que se puede mostrar a los alumnos.
Contenidos:
- El soporte como espacio para la representación bidimensional.
- Las posibilidades de las distintas dimensiones y formatos.
- Relación entre la organización de la imagen y las características del soporte.
- El encuadre de la imagen.
- Los límites de la representación y su inclusión en el espacio del soporte.
- Distintas calidades de los soportes.
- Texturas y colores.
- Relación entre las características de los materiales de trabajo y las calidades de los soportes.
El tema:
Respecto del tema, cada alumno buscará uno de su interés entre los muchos posibles: un conjunto de objetos encontrados al azar o preparados especialmente, un retrato en interiores, un retrato al aire libre, un paisaje de interior o de exterior, la captación del movimiento (si se está trabajando con cámara de fotos), etc.
El encuadre:
Respecto del encuadre será conveniente acompañar a los alumnos en la exploración de la porción de imagen que quieren mostrar y en cómo ubicarán los distintos elementos dentro del cuadro (por ejemplo, si un chico decidió dibujar o fotografiar un árbol, tendrá que decidir si éste quedará ubicado en el centro, a la izquierda o a la derecha, si se verá completo o en forma parcial, etc.).
Los puntos de vista:
Será interesante que docente y alumnos exploren juntos las posibilidades que ofrecen los distintos puntos de vista, especialmente los no tan convencionales, como por ejemplo aquellos donde los objetos son 'mirados' desde arriba o desde abajo, o vistos en ángulos diversos, etc.
La toma:
Si tienen la posibilidad de tomar fotografías, y de acuerdo con la imagen elegida, cada uno podrá evaluar la conveniencia de realizar la toma en sentido horizontal o vertical. Las mismas pautas son aplicables a la realización de dibujos.
Luego de todo este trabajo previo, tanto en un dibujo como en la toma fotográfica se captará la imagen y, a través de la observación, los alumnos analizarán los resultados poniendo el acento en la relación entre el encuadre -en tanto recorte espacial-, el punto de vista y la manera de centrar lo que se ve a través de la "ventana".


QUE ES LA ROTACIÓN, TRASLACIÓN Y ESCALACION:
Introducción
Todo cuerpo representado en un plano puede sufrir varios tipos de transformaciones en su estructura. Las transformaciones de tipo básico, como pueden ser la translación, Escalación y rotación de objetos.
Un objeto definido se construye a partir de una serie de puntos coordenados, desde los cuales se pueden aplicar diversas fórmulas para realizar un cambio de la figura.
Traslación, Rotación, Escalación
Traslación
Se pueden encontrar varias definiciones de traslación
Una traslación es el movimiento en línea recta de un objeto de una posición a otra.
Movimiento de una figura, sin rotarla ni voltearla. "Deslizar".
La figura sigue viéndose exactamente igual, solo que en un lugar diferente.
Se aplica una transformación en un objeto para cambiar su posición a lo largo de la trayectoria de una línea recta de una dirección de coordenadas a otra.
Ejemplos

Rotación
Para rotar un objeto (en este caso bidimensional), se ha de determinar la cantidad de grados en la que ha de rotarse la figura. Para ello, y sin ningún tipo de variación sobre la figura, la cantidad de ángulo ha de ser constante sobre todos los puntos.
Otra forma de conseguir la rotación, respecto a un punto de movimiento, es fijar los diferentes puntos respecto a un punto de fijación siendo los puntos que forman la figura, relativos a este.
La fórmula a aplicar en este último supuesto, sería la siguiente:
X' = X * Cos (àngulo) - Y * Sin(ángulo)
Y' = Y * Cos (ángulo) - X * Sin(ángulo)
Ejemplos
Escalación
Una transformación para alterar el tamaño de un objeto se denomina escalación.
Dependiendo del factor de escalación el objeto sufrirá un cambio en su tamaño pasando a ser mayor, o menor en su segmento de longitud.
Esta es la transformación del objeto especialmente interesante, pues con ella se consigue el efecto Zoom.
Ejemplos:
Bibliografía
• http://encanta.avalonsoftware.org/idgaw/09/animvect2.php
• http://www.mitecnologico.com/Main/Escalacion
• http://encanta.avalonsoftware.org/idgaw/09/animvect2.php
__________________________________________________________________________________
COMPOSICIÓN DE TRANSFORMACIONES BIDIMENSIONALES
(Traslación, Escalación y Rotación)
Introducción
Transformaciones como la traslación, rotación y escalado permiten simular el movimiento de los objetos, así como situar los objetos.
Transformación “Traslación”: Trasladar un objeto complejo requiere trasladar únicamente los vértices que lo componen. En las nuevas posiciones vuelven a unirse los vértices.
Trasladar un objeto complejo requiere trasladar únicamente los vértices que lo componen. En las nuevas posiciones vuelven a unirse los vértices.
A los valores dx y dy se les denomina distancias de traslación. Estas distancias son números reales positivos o negativos.
Transformación “Escalación”:
La operación de escalado modifica la distancia de los puntos sobre los que se aplica, respecto a un punto de referencia.
Para definir esta operación son necesarios dos factores de escala, Sx y Sy, según las direcciones x e y, y un punto o eje de referencia.
Existen dos tipos de escalado:
Escalado uniforme: El factor de escala es el mismo en las dos coordenadas, es decir Sx=Sy, y por lo tanto varía el tamaño pero no la forma del objeto.
Escalado diferencial: El factor de escala es distinto en cada dirección, es decir Sx es distinto de Sy, y se produce una distorsión en la forma del objeto.
Transformación “Rotación”:

Determina la rotación considerando un punto que se encuentra a una distancian del origen R y esta distancia forma el ángulo con la horizontal.
Conclusión:
Nosotros entendimos que composición de transformaciones bidimensionales es la mezcla de la composición de transformaciones como son la traslación, la escalación, y la rotación, que son útiles para la creación de efectos sobre imágenes.
TRAZADO DE LINEAS RECTAS:
Trazado de líneas:
Diferentes tipos de líneas y situaciones en que se dibujan se resuelven con técnicas diferentes.
- Líneas cortas, o líneas que corren paralelas a otras que nos sirven de referencia.
- Líneas largas. Es el caso de líneas que unen dos puntos alejados, sin ninguna otra referencia. Las primeras líneas de cualquier croquis entran en esta categoría.
Líneas cortas o líneas paralelas a otras ya existentes se las puede dibujar de un solo trazo. Primero se deben mirar bien los puntos de inicio y terminación para luego ejecutar el trazo.
Para el trazado de líneas largas vamos a dar tres técnicas que se utilizarán según las circunstancias.
Líneas punto a punto:
La técnica más rápida es, una vez determinados los puntos a unir se comienza moviendo el lápiz desde uno de ellos hacia el otro. Mientras se hace este movimiento se debe mantener la vista sobre el punto de destino. Esto último nos permitirá conservar la dirección.
Líneas compuestas:
Una segunda técnica es proceder mediante trazos de cinco a siete centímetros; como si se estuviesen dibujando una sucesión de líneas más cortas. La interrupción del trazo permite verificar el rumbo del trazo y se corregir si es necesario. Los trazos sucesivos no se superponen a fin de posibilitar uniformidad de espesor. Se deja una pequeñísima luz entre ellos de forma tal que apenas resulte perceptible la interrupción y mantenga el espesor uniforme. [dibujo de ejemplo]
Líneas de construcción:
Una tercera técnica, particularmente aplicable cuando se está planteando el dibujo, es utilizar líneas de tanteo. Resulta un poco más lenta que las anteriores, pero es de gran ayuda para obtener líneas rectas particularmente cuando son muy largas. Consiste en insinuar la línea en forma apenas visible con trazos muy suaves. Idealmente, solo el dibujante debería percibir esos trazos de tanteo. Se observa el resultado obtenido. Se introducen las correcciones necesarias hasta lograr definir el trayecto correcto. Entonces se comienza el trazado de la línea en forma similar al primer método, pero ahora con una guía visual. Si fuese necesario, porque se utilizaron demasiadas líneas de tanteo, se podrán borrar las que no sirven, antes del trazado definitivo.
Modelo de Representación Polígonal sobre OpenGL:
La librería gráfica OpenGL es por naturaleza una librería orientada al trabajo con modelos poliédricos, por tanto nos será fácil realizar representación de esta naturaleza. Puntualizaremos que se trata de una librería de funciones orientada principalmente a modelos interactivos, por ello se premia la rapidez frente al espacio, el tipo de representación poligonal que empleara será por tanto explícita.
Las definiciones de primitivas poligonales en OpenGL se encierran entre las llamadas a las funciones:
glBegin(GLEnum tipo_primitiva) y glEnd(void). Entre dichas funciones deberemos especificar la lista de vértices que componen nuestro polígono. La función para pasar las coordenadas de cada vértice es glVertex3fv(GLFloat *coor), donde ‘coor’ es un vector que contiene las tres coordenadas del vértice.
Los valores normales para el tipo de primitiva son las constantes:
Valor de la Cte GL Tipo de Primitiva Poligonal:
GL_POINTS Puntos aislados
GL_LINES Líneas de dos vértices
GL_LINE_STRIP Línea de cualquier numero de vértices
GL_LINE_LOOP Línea Cerrada.
GL_POLYGON Polígono de Cualquier tipo
GL_TRIANGLES Polígonos de tres lados
GL_TRIANGLE_STRIP Tira de Triangulos
GL_QUADS Polígonos de cuatro vertices
GL_QUAD_STRIP Tira de Cuadrilateros.
GL_TRIANGLE_FAN Abanico de triangulos.
Algoritmo de Línea DDA:
El analizador diferenciador digital (DDA - Digital Differential Analyzer) es un algoritmo de conversion de rastreo que se basa en el calculo ya sea de Dy o Dx por medio de las ecuaciones (4) o (5).
Se efectúa un muestreo de la línea en intervalos unitarios en una coordenada y se determina los valores enteros correspondientes mas próximos a la trayectoria de la línea para la otra coordenada.
Tomemos una línea con pendiente positiva, si la pendiente | m | £ 1, se hace el muestreo en x en intervalos unitarios (Dx = 1 y Dy = m dado que m = Dy / Dx) y se calcula cada valor sucesivo de y como:
(6) yk+1 = yk+ m
El subíndice toma valores enteros a partir de 1 y aumenta a razón de 1 hasta alcanzar el valor final.
Ya que m puede ser cualquier numero real entre 0 y 1, los valores calculados de y deben redondearse al entero mas
cercano.
Para líneas con una pendiente | m | > 1, se revierten las funciones de x y y, o sea, se realiza un muestreo de y en intervalos unitarios (Dy = 1 y Dx = 1/m dado que m = Dy /Dx) y se calcula cada valor sucesivo de x como:
(7) xk+1 = xk+ 1/m
Las ecuaciones (6) y (7) se basan en la suposición de que las líneas deben procesarse del extremo izquierdo al derecho.
Si este procesamiento se revierte, entonces Dx o Dy serian -1, y
yk+1 = yk - m o xk+1 = xk - 1/m
El procedimiento completo de dibujo seria el siguiente:
void Line(Display* display, Window win, GC gc, int x0, int y0, int x1, int y1)
{
float x, y, xs, ys;
int dx, dy, steps;
dx = x1 - x0;
dy = y1 - y0;
/* se asigna el punto de donde se comenzara a dibujar la línea */
x = x0;
y = y0;
/* verificar si la pendiente es mayor de x o y, para luego asignarla a steps */
if (abs(dx) > abs(dy))
steps = abs(dx);
else
steps = abs(dy);
/* se divide por la pendiente mayor, para dar xs o ys igual a 1 (o -1) */
Alfredo Weitzenfeld Gráfica: Línea 3
if (steps == 0) {
XDrawPoint(display,win,gc,round(x),round(y));
fprintf(stderr,”this line is a point”);
return;
}
xs = dx/steps;
ys = dy/steps;
/* se cicla uno a la vez hasta llegar al numero de steps máximo */
for (i = 0; i <= steps; i++)
{
XDrawPoint(display,win,gc,round(x),round(y)); /* round(x) -> x+0.5 */
x = x + xs;
y = y + ys;
}
}
Algoritmo de Línea Bresenham Básico:
Un algoritmo preciso y efectivo para la generación de líneas de rastreo, desarrollado por Bresenham (1965), convierte mediante rastreo las líneas utilizando solo cálculos incrementales con enteros que se pueden adaptar para desplegar también curvas.
El algoritmo busca cual de dos pixeles es el que esta mas cerca según la trayectoria de la línea.
Consideremos el proceso de conversion para líneas con pendiente positiva 0 < m < 1.
Las posiciones de pixel a lo largo de la trayectoria de una línea se determinan al efectuar un muestreo de x en intervalos unitarios.
Si se inicia desde el extremo izquierdo (x0,y0) de una línea determinada, se pasa a cada columna sucesiva y se traza el pixel cuyo valor de y se aproxima mas a la trayectoria de la línea de rastreo.
Si suponemos que se debe desplegar el pixel en (xk,yk), a continuación se necesita decidir que pixel se debe desplegar en la columna xk+1.
Las alternativas son los pixeles (xk+1,yk), y (xk+1,yk+1).
Al realizar el muestreo en la posición xk+1 designamos la separación de pixeles verticales de la trayectoria de la línea matemática como d1 y d2.
REPRESENTACIÓN Y TRAZADO DE POLÍGONOS:
Polígono
Un polígono es una figura bidimensional compuesta por una secuencia finita de segmentos rectos consecutivos que cierran una región en el espacio. Estos segmentos son llamados lados, y los puntos en que se intersecan se llaman vértices. El interior del polígono es llamado área.
 |  | 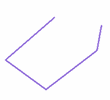 |
Polígono
(lados rectos) | No es un polígono
(tiene una curva) |
No es un polígono
(abierto, no cerrado) |
Tipos de polígonos:
Un polígono simple sólo tiene un borde que no se cruza con él mismo. Uno complejo se interseca consigo mismo.
 | 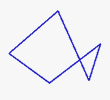 |
Polígono simple
(este es un pentágono) | Polígono complejo
(también es un pentágono) |
Un polígono convexo no tiene ángulos que apunten hacia dentro. En concreto, los ángulos internos no son mayores que 180°.
Si hay algún ángulo interno mayor que 180° entonces es cóncavo.
 |  |
| Convexo | Cóncavo |
Si todos los ángulos son iguales y los lados también, es regular, si no es irregular
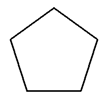 |  |
| Regular | Irregular |
Analizador Diferencial Digital:
Una implementación de hardware o software de un Analizador Diferencial Digital (DDA) se usa para la interpolación lineal de variables sobre un intervalo entre un punto de comienzo y un punto de fin. Los DDAs se usan para rastreo de lineas, triangulos y polígonos. En la implementación mas simple del algoritmo DDA interpola valores en intervalo [(xinicio, yinicio), (xfin, yfin)] por calculo para cada xi las ecuaciones xi = xi−1+1, yi = yi−1 + Δy/Δx, donde Δx = xfin − xinicio y Δy = yfin − yinicio.
Si m>=0 (pendiente positiva)
Si m<=1
de izquierda a derecha
* muestreo de x (Δx =1)
* yk+1 = redondeo(yk + m) k=1,2,...
de derecha a izquierda
* muestreo de x (Δx =-1)
* yk+1 = redondeo(yk - m) k=1,2,...
Si m > 1 (para evitar la aparición de agujeros)
de izquierda a derecha
* muestreo de y (Δy =1)
* xk+1 = redondeo(xk + 1/m) k=1,2,...
de derecha a izquierda
* muestreo de y (Δy =-1)
* xk+1 = redondeo(xk - m) k=1,2,...
Si m<0 (pendiente negativa)
Si |m|<1
de izquierda a derecha
* muestreo de x (Δx =1)
* yk+1 = redondeo(yk + m) k=1,2,...
de derecha a izquierda
* muestreo de x (Δx =-1)
* yk+1 = redondeo(yk - m) k=1,2,...
Si |m| > 1 (para evitar la aparición de agujeros)
de izquierda a derecha
* muestreo de y (Δy =1)
* xk+1 = redondeo(xk + 1/m) k=1,2,...
de derecha a izquierda
* muestreo de y (Δy =-1)
* xk+1 = redondeo(xk - m) k=1,2,...


.jpg)

REPRESENTACIÓN MATRICIAL:
En las aplicaciones de diseño y de creación de imágenes, realizamos traslaciones, rotaciones y escalaciones para ajustar los componentes de la imagen en sus posiciones apropiadas. En este tema consideramos cómo se pueden volver a formular las representaciones de la matriz de modo que se pueden procesar de manera eficiente esas secuencias de transformación. Es posible expresar cada una de las transformaciones básicas en la forma de matriz general con las posiciones de coordenadas P y P’ representadas como columnas de vector.
Con las representaciones de matriz podemos establecer una matriz para cualquier secuencia de transformaciones como una matriz de transformación compuesta al calcular el producto de la matriz de las transformaciones individuales. La creación de productos de matrices de transformación a menudo se conoce como concatenación o composición de matrices.
Se se aplican dos vectores de traslación sucesivos (tx1, t y1) y (tx2 , t y2 ) en la posición de coordenadas P, la localización transformada final P, la localización transformada final P’ se calcula como: P'=T(t x2,t2)·T(tx1,ty1)·P}{=T(tx2, 2)·T(t x1,t y1)}{·P
Donde se representan P y P’ como vectores de columna de coordenadas homogéneas. Podemos verificar este resultado al calcular el producto de la matriz para las dos agrupaciones asociativas. Asimismo, la matriz de transformación compuesta para esta secuencia de transformaciones.
Dos rotaciones sucesivas que se aplican en el punto P producen la posición transformada P'=R(θ2)·R(θ1){·P}=R(θ2){· (θ1)}·P
Al multiplicar las dos matrices de rotación, podemos verificar que dos rotaciones sucesivas son aditivas
La siguiente figura ilustra una secuencia de transformación para producir escalación con respecto de una posición fija seleccionada (xf,f) al utilizar una función de escalación que sólo puede escalar en relación con el origen de las coordenadas
Propiedades de concatenación
La multiplicación de matrices es asociativa. Para tres matrices cualesquiera A, B y C, el producto matricial A·B·C se puede llevar a cabo al multiplicar primero a por B o multiplicar primero B por C:2.35.A · BC=( A· B)·C =A·( B·C)
Por tanto, podemos evaluar los productos matriciales al utilizar una agrupación asociativa ya sea de izquierda a derecha o de derecha a izquierda. Por otro lado, los productos de la transformación tal vez no sean conmutativos. En general el producto matricial A·B no es igual que B·A. Esto significa queremos trasladar y girar un objeto, debemos tener cuidado sobre el sentido en que se evalúa la matriz compuesta.
VENTANA Y PUERTO DE VISIÓN:
Un área rectangular que se especifica en coordenadas mundiales se denomina ventana. El área rectangular en el dispositivo de despliegue en el cual se coloca la ventana se llama puerta de visión. La figura ilustra el trazo o planimetría de la selección de una imagen que queda dentro del área de ventana en una puerta de visión designada. Esta planimetría se llama transformación de la visión o bien transformación de normalización.
Los límites de la ventana se especifican en coordenadas mundiales. Las coordenadas de dispositivo normalizadas se usan con mayor frecuencia para la especificación de la puerta visión, aunque las coordenadas del dispositivo pueden emplearse si hay solamente un dispositivo de salida en el sistemas. Cuando se usan coordenadas de dispositivo normalizadas, el programador considera el dispositivo de salida como aquel que tiene valores coordenados dentro del intervalo de 0 a 1.
Las posiciones de coordenadas que se expresan en coordenadas de dispositivo normalizadas deben convertirse a las coordenadas del dispositivo antes de que un dispositivo de salida específico haga el despliegue. Una rutina específica del dispositivo se incluye en paquetes de gráficas con este fin. La ventaja de emplear coordenadas de dispositivo normalizadas es que el paquete de gráficas es considerablemente independiente del dispositivo. Pueden utilizarse distintos dispositivos de salida ofreciendo los conductores adecuados del dispositivo.
Cambiando la posición de la puerta de visión, los objetos pueden desplegarse en diferentes posiciones en un dispositivo de salida. Asimismo, variando el tamaño de las puertas de visión, el tamaño y las proporciones de los objetos pueden alterarse. Cuando se trazan en forma sucesiva ventanas de diferentes tamaños en una puerta de visión, pueden lograrse efectos de acercamiento. Conforme las ventanas se hacen pequeñas, un usuario puede lograr el acercamiento de alguna parte de una escena para visualizar detalles que no se muestran con las ventanas mayores.
Analógicamente, puede obtener un panorama general más amplio realizando un acercamiento de una sección de escena con ventanas cada vez más mayores. Los efectos de toma panorámica se producen moviendo o desplazando una ventana de tamaño fijo a través de una imagen grande.







.jpg)































.jpg)
.jpg)










.jpg)









