Unidad 2
-Trazos de lineas rectas
Conclusión:
Cuando hablamos de Graficación en 2 dimensiones, lo primero que se nos viene a la mente es un gráfico cartesiano(o de tipo X-Y), siendo de común aplicación para la mayor parte de las ciencias al graficar alguna función respecto a algo. Sin embargo, la Graficación en 2D tiene más aplicaciones implícitas en muchas aplicaciones como páginas web (al mostrar cualquier imagen), al dibujar cualquier figura geométrica tanto regular como irregular en algún programa que lo permita, al diseñar alguna estructura preliminar o los trazos de dicha estructura.
Simplemente, el trazado de una línea, requiere un algoritmo (en mi opinión, algoritmo matemático) que aproxima dichas primitivas gráficas (ideales), a un conjunto de pixeles en cierto ambiente. Estos pixeles son almacenados como mapas de bits en un buffer de memoria gráfica y son dibujadas por algún lienzo de cierto programa gráfico.
Desde luego esto no queda limitado, pues el diseño de diversos polígonos (regulares e irregulares) y figuras geométricas requieren de ciertos algoritmos, anexadas las propiedades de ciertas figuras geométricas (el punto de unión, los lados de las figuras, ángulos internos, etc.). Y la Graficación en dos dimensiones facilita la representación de estas figuras para poder diseñar o plasmar modelos, graficas e imágenes que se deseen.
Pero a veces se necesita realizar ciertas manipulaciones a las figuras, respecto a un ambiente de Graficación, mencionando las principales: como la escalación de menor o mayor volumen, la rotación a una dirección, y la traslación de un punto a otro de las figuras en un mapa de bits, entre otras derivaciones, y son llamadas transformaciones bidimensionales. Y por supuesto que, estas operaciones están representadas matemáticamente, y comúnmente se representa en matrices (representación matricial) donde se explica con matemáticas, el comportamiento de la operación aplicada en una figura, o la encadenación de operaciones sucesivas a petición del usuario.
Incluso, todo esto está contemplado en el momento de la representación grafica en pantalla, con determinado punto de vista de la figura y la pantalla junto con el margen de visión para que el usuario pueda observar de manera óptima los gráficos que esta diseñando o manipulando.
-Representación y trazo de poligonos
-Transformaciones Bidimencionales
-Representación matricial
-Ventana y puerto de visión
Conclusión:
Cuando hablamos de Graficación en 2 dimensiones, lo primero que se nos viene a la mente es un gráfico cartesiano(o de tipo X-Y), siendo de común aplicación para la mayor parte de las ciencias al graficar alguna función respecto a algo. Sin embargo, la Graficación en 2D tiene más aplicaciones implícitas en muchas aplicaciones como páginas web (al mostrar cualquier imagen), al dibujar cualquier figura geométrica tanto regular como irregular en algún programa que lo permita, al diseñar alguna estructura preliminar o los trazos de dicha estructura.
Simplemente, el trazado de una línea, requiere un algoritmo (en mi opinión, algoritmo matemático) que aproxima dichas primitivas gráficas (ideales), a un conjunto de pixeles en cierto ambiente. Estos pixeles son almacenados como mapas de bits en un buffer de memoria gráfica y son dibujadas por algún lienzo de cierto programa gráfico.
Desde luego esto no queda limitado, pues el diseño de diversos polígonos (regulares e irregulares) y figuras geométricas requieren de ciertos algoritmos, anexadas las propiedades de ciertas figuras geométricas (el punto de unión, los lados de las figuras, ángulos internos, etc.). Y la Graficación en dos dimensiones facilita la representación de estas figuras para poder diseñar o plasmar modelos, graficas e imágenes que se deseen.
Pero a veces se necesita realizar ciertas manipulaciones a las figuras, respecto a un ambiente de Graficación, mencionando las principales: como la escalación de menor o mayor volumen, la rotación a una dirección, y la traslación de un punto a otro de las figuras en un mapa de bits, entre otras derivaciones, y son llamadas transformaciones bidimensionales. Y por supuesto que, estas operaciones están representadas matemáticamente, y comúnmente se representa en matrices (representación matricial) donde se explica con matemáticas, el comportamiento de la operación aplicada en una figura, o la encadenación de operaciones sucesivas a petición del usuario.
Incluso, todo esto está contemplado en el momento de la representación grafica en pantalla, con determinado punto de vista de la figura y la pantalla junto con el margen de visión para que el usuario pueda observar de manera óptima los gráficos que esta diseñando o manipulando.
2.1 Trazo de lineas rectas
Trazo de lineas rectas.
Primero debemos definir algunos conceptos como punto, linea y trazo
Punto: (Del lat. punctum). Señal de dimensiones pequeñas, ordinariamente circular, que, por contraste de color o de relieve, es perceptible en una superficie.
Linea: Trazo largo y continuo en una sola dirección, la que permanecerá invariable durante toda su extensión.
Trazo: Delineación con que se forma el diseño o planta de cualquier cosa.
Por lo que podemos confirmar, el puno es una "señal" muy pequeña con forma circular originalmente y perceptible a simple vista; y la unión sucesiva de éstos forma una linea que tiene una dirección, magnitud, un punto de origen (DONDE SE INICIA EL TRAZO DE LA RECTA ) y punto final (HASTA DONDE LLEGA EL TRAZO); y al aplicarse estos elementos en algún gráfico o imagen, describe un contorno o un borde al que se llama trazo.
Estos elementos son tan importantes y básicos cualquier arte, técnica o ciencia que necesita plasmar un algo en una superficie.
Las formas de graficar una linea.
Hay dos tipos básicos de gráficos: Imágenes en mapa de bits (o rasterizadas) e imágenes vectoriales. En el primer caso, a continuación, se hablara de rectas rasterizadas.
Algoritmo DDA (Analizador Diferencial Digital) para generación de líneas.
DDA: El Algoritmo DDA es un algoritmo de línea de conversión de rastreo que se basa en el cálculo ya sea en el incremento de X o en el incremento de Y. La finalidad de este algoritmo es determinar los valores enteros correspondientes más próximos a la trayectoria de la línea para la otra coordenada.
Algoritmo de Bresenham
El algoritmo de Bresenham se generaliza para líneas con una pendiente arbitraria al considerar la simetría entre los diversos octantes y cuadrantes del plano de xy.
Para una línea con una pendiente m > 1, intercambiamos las funciones de las direcciones de x y y, o sea, pasamos a lo largo de y en pasos unitarios y calculamos los valores sucesivos de x que se aproximan mas a la trayectoria de la línea. Asimismo, podemos revisar el programa para trazar píxeles iniciando desde cualquier extremo.
Explicando el algoritmo.
Si 0<|m|<1 (m mayor que 0 y menor que 1)
1.- Capturar los extremos de la línea y se almacena el extremo izquierdo en las coordenadas (x0,y0) que es el origen del sistema de coordenadas.
2.- Se carga las coordenadas (x0,y0) en el buffer de estructura donde se trazara el primer punto.
3.- Se calculan las constantes Δx ,Δy, 2Δy y 2Δy-Δx (Δx es lo mismo que decir, incremento en x) y se obtiene el valor inicial para el parámetro de decisión con la siguiente formula p0=2Δy-Δx.
Para j=0 (j es una variable auxiliar), mientras j<Δx (j mayor que incremento en x).
--En cada xk a lo largo de la línea, que inicia en k=0 se efectúa la prueba siguiente:
Si pk<0
--Trazamos (xk+1,yk).
--Asignamos pk+1= pk+2Δy.
Si no se cumple.
--Trazamos (xk+1,yk+1).
--Asignamos pk+1= pk+2Δy-2Δx.
Pero si |m|>1
*Recorremos la dirección en pasos unitarios y calculamos los valores sucesivos
de x que se aproximen más a la trayectoria de la línea.
Fuentes:
1.-Apuntes sobre Representación Gráfica.
2.-Gráficos Vectoriales
3.-Computación Gráfica y Visual
4.-¿Qué son los gráficos vectoriales?
Lados:
Los valores normales para el tipo de primitiva son las constantes:
Transformaciones Geométricas Básicas.
En este apartado veremos las operaciones de transformación que se pueden aplicar a objetos para reubicarlos o dar es un tamaño diferente.
Estas operaciones también son usadas en la visualización de rutinas que convierten una descripción de un sistema de coordenadas universales en un despliegue para un dispositivo de salida. Además, son usados en variedad de otras aplicaciones, tales como diseño de ayuda y animación por computador. Las operaciones que se aplican a descripciones geométricas de un objeto para cambiar su posición, orientación o tamaño se llaman transformaciones geométricas entre otras.
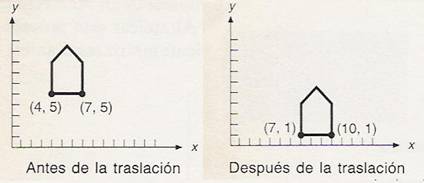
Traslación
Reposiciona un objeto desplazándolo a las nuevas coordenadas, en otras palabras, una traslación se aplica a un objeto para reposicionarlo a lo largo de una línea recta, desde una ubicación de coordenadas a otra.
Representándola en forma cartesiana.
P = (x, y) P'= (x', y')
T = (tx, ty) "El par (t subindice x, t subindice y) se llama vector de traslación"
Representándola en forma matricial.
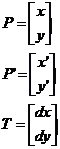
Esto nos permite escribir las ecuaciones de traslación bidimensionales en forma de matriz
para obtener: P'= P +T
Al trasladar cualquier objeto dentro del mundo virtual se debe considerar lo siguientes puntos:
• Es una transformación rígida, el objeto no se deforma
• Para trasladar líneas rectas trasladamos sólo sus extremos
• Para trasladar polígonos, trasladamos sólo sus vértices y redibujamos.
Reflexión
Una transformación que produce la imagen de un objeto en un espejo se llama reflexión. Para una reflexión bidimensional, esta imagen se genera respecto a un eje de reflexión rotando el objeto 180° sobre dicho eje de reflexión.
Esto se puede conseguir con una rotación en 180º, alrededor del eje x ó en el eje y.
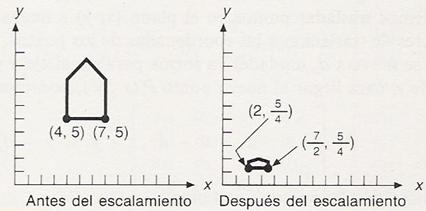
Escalación
La transformación de la escalación altera el tamaño del objeto, esto lo hace escalando
cada uno de sus coordenadas con respecto al origen del eje de coordenadas
Definiendo las coordenadas
x′= x*Sx y′= y*Sy
Sx es la escala en la dirección en x y Sy es la escala en la dirección en y.
donde los parámetros de escalación Sx y Sy se asignan cualesquiera valores positivos.
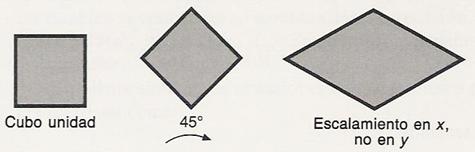
Escalamiento en cualquier dirección
Los parámetros Sx y Sy escalan un objeto en las direcciones x e y respectivamente.
Se puede escalar un objeto en otra dirección, rotando el objeto y alineándolo con el sistema de coordenadas y luego rotándolo en sentido inverso.
Descrito en la siguiente imagen con su respectiva ecuación:
• Para escalar polígonos, escalamos sólo sus vértices y redibujamos.
Rotación
En rotación, la orientación de ésta puede ser especificada en una variedad de formas, lo que se
explica a continuación es la rotación de un punto con respecto a los ejes fijos. Un eje de
rotación define el polo sobre el cual se va a rotar, como los polos Norte y Sur de la Tierra.
x = r cos teta
y = r sen teta
Rotación alrededor de un punto
Para hacer una rotación general, podemos hacerlo mediante una composición de
transformaciones básicas.
Para generar una rotación se especifica un ángulo de rotación θ y laposición (xr, yr) del punto de rotación (punto pivote) acerca del cual el objeto se rota.
Valores positivos del ángulo de rotación definen una rotación en contra de las agujas del reloj y lo contrario para un ángulo negativo.
En representacion matricial:
P′= R*P
Fuentes
1.-Transformaciones Geometricas
2.-TEMA 3: Transformaciones 2D
3.-CAPÍTULO III: TRANSFORMACIONES GEOMÉTRICAS
4.-CAPITULO 1 Transformaciones Geométricas en dos dimensiones
5.-CAPÍTULO 2 – Modelado y Transformaciones Geométricas
Primero debemos definir algunos conceptos como punto, linea y trazo
Punto: (Del lat. punctum). Señal de dimensiones pequeñas, ordinariamente circular, que, por contraste de color o de relieve, es perceptible en una superficie.Trazo: Delineación con que se forma el diseño o planta de cualquier cosa.Por lo que podemos confirmar, el puno es una "señal" muy pequeña con forma circular originalmente y perceptible a simple vista; y la unión sucesiva de éstos forma una linea que tiene una dirección, magnitud, un punto de origen (DONDE SE INICIA EL TRAZO DE LA RECTA ) y punto final (HASTA DONDE LLEGA EL TRAZO); y al aplicarse estos elementos en algún gráfico o imagen, describe un contorno o un borde al que se llama trazo.
Estos elementos son tan importantes y básicos cualquier arte, técnica o ciencia que necesita plasmar un algo en una superficie.
Las formas de graficar una linea.
Hay dos tipos básicos de gráficos: Imágenes en mapa de bits (o rasterizadas) e imágenes vectoriales. En el primer caso, a continuación, se hablara de rectas rasterizadas.
Algoritmo DDA (Analizador Diferencial Digital) para generación de líneas.
DDA: El Algoritmo DDA es un algoritmo de línea de conversión de rastreo que se basa en el cálculo ya sea en el incremento de X o en el incremento de Y. La finalidad de este algoritmo es determinar los valores enteros correspondientes más próximos a la trayectoria de la línea para la otra coordenada.
Una implementación de hardware o software de un Analizador Diferencial Digital (DDA) se usa para la interpolación lineal de variables sobre un intervalo entre un punto de comienzo y un punto de fin.
Los DDAs se usan para rastreo de lineas, triángulos y polígonos. En la implementación mas simple del algoritmo DDA interpola valores en intervalo [(xinicio, yinicio), (xfin, yfin)] por calculo para cada xi las ecuaciones xi = xi−1+1, yi = yi−1 + Δy/Δx, donde Δx = xfin − xinicio y Δy = yfin − yinicio.
Explicando el algoritmo.
Si m>=0 (pendiente positiva)
Si m<=1
de izquierda a derecha
* muestreo de x (Δx =1)
* yk+1 = redondeo(yk + m) k=1,2,...
de derecha a izquierda
* muestreo de x (Δx =-1)
* yk+1 = redondeo(yk - m) k=1,2,...
Si m > 1 (para evitar la aparición de agujeros)
de izquierda a derecha
* muestreo de y (Δy =1)
* xk+1 = redondeo(xk + 1/m) k=1,2,...
de derecha a izquierda
* muestreo de y (Δy =-1)
* xk+1 = redondeo(xk - m) k=1,2,...
Si m<0 (pendiente negativa)
Si |m|<1
de izquierda a derecha
* muestreo de x (Δx =1)
* yk+1 = redondeo(yk + m) k=1,2,...
de derecha a izquierda
* muestreo de x (Δx =-1)
* yk+1 = redondeo(yk - m) k=1,2,...
Si |m| > 1 (para evitar la aparición de agujeros)
de izquierda a derecha
* muestreo de y (Δy =1)
* xk+1 = redondeo(xk + 1/m) k=1,2,...
de derecha a izquierda
* muestreo de y (Δy =-1)
* xk+1 = redondeo(xk - m) k=1,2,...
El algoritmo de Bresenham se generaliza para líneas con una pendiente arbitraria al considerar la simetría entre los diversos octantes y cuadrantes del plano de xy.
Para una línea con una pendiente m > 1, intercambiamos las funciones de las direcciones de x y y, o sea, pasamos a lo largo de y en pasos unitarios y calculamos los valores sucesivos de x que se aproximan mas a la trayectoria de la línea. Asimismo, podemos revisar el programa para trazar píxeles iniciando desde cualquier extremo.
Explicando el algoritmo.
Si 0<|m|<1 (m mayor que 0 y menor que 1)
1.- Capturar los extremos de la línea y se almacena el extremo izquierdo en las coordenadas (x0,y0) que es el origen del sistema de coordenadas.
2.- Se carga las coordenadas (x0,y0) en el buffer de estructura donde se trazara el primer punto.
3.- Se calculan las constantes Δx ,Δy, 2Δy y 2Δy-Δx (Δx es lo mismo que decir, incremento en x) y se obtiene el valor inicial para el parámetro de decisión con la siguiente formula p0=2Δy-Δx.
Para j=0 (j es una variable auxiliar), mientras j<Δx (j mayor que incremento en x).
--En cada xk a lo largo de la línea, que inicia en k=0 se efectúa la prueba siguiente:
Si pk<0
--Trazamos (xk+1,yk).
--Asignamos pk+1= pk+2Δy.
Si no se cumple.
--Trazamos (xk+1,yk+1).
--Asignamos pk+1= pk+2Δy-2Δx.
Pero si |m|>1
*Recorremos la dirección en pasos unitarios y calculamos los valores sucesivos
de x que se aproximen más a la trayectoria de la línea.
Algoritmo de Xiaolin Wu
El algoritmo de Xiaolin Wu es una mejora del algoritmo de Bresenham que permite dibujar rectas en dispositivos de gráficos rasterizados reduciendo el aliasing. El algoritmo se basa en dibujar parejas de pixeles a lo largo del trazado de la recta con diferentes intensidades en función de la cercanía a la recta real.
Gráficos Vectoriales
Un gráfico vectorial es toda imagen digital formada por diferentes objetos geométricos independientes. Cada uno de estos elementos definido por parámetros matemáticos como la forma, posición, color, el tipo y grosor de contorno, etc.
Los gráficos vectoriales son en su formato completamente distintos a los gráficos de mapas de bits o también llamados matriciales, los cuales están constituidos por pixeles.
Los vectores tienen la ventaja sobre los pixeles de ser escalables, es decir, se puede aumentar su tamaño conservando su calidad original. Lo que no ocurre con los gráficos a base de pixeles que presentan degradación de la calidad al aumentar el tamaño.
Fuentes:
1.-Apuntes sobre Representación Gráfica.
2.-Gráficos Vectoriales
3.-Computación Gráfica y Visual
4.-¿Qué son los gráficos vectoriales?
2.2 Representación y trazo de poligonos
Representación de los polígonos
Polígono es la superficie plana encerrada dentro de un contorno formado por segmentos rectos unidos en sus extremos.
- Cada uno de los segmentos se denomina lado.
- El punto de unión de cada par de segmentos se denomina ángulo.
- El numero de lados, ( y por tanto de ángulos) ha de ser mayor o igual a tres.
Elementos de un polígono
Lados:
Son los segmentos que lo limitan.
Vértices
Son los puntos donde concurren dos lados.
Ángulos interiores de un polígono
Son los determinados por dos lados consecutivos.
El polígono es el caso bidimensional del politopo, figura geométrica general definida para cualquier número de dimensiones. a noción geométrica elemental ha sido adaptada de distintas maneras para servir a propósitos específicos.
En Matemáticas, un politopo regular es una figura geométrica con un alto grado de simetría. Ejemplo de politopos regulares en dos dimensiones son el cuadrado, el pentágono y el hexágono regular.
La representación básica de alguna imagen se limita a polígonos regulares e irregulares formados por vértices.
Se pueden organizar los polígonos para mejorar el tratamiento.
Ahora que se ha aclarado el concepto y los elementos básicos de un polígono y su generalización (politopo) podemos centrarnos en la construcción de polígonos en algún ambiente de graficación.
Dibujando Poligonos con OpenGL
OpenGL tiene únicamente unas pocas primitivas geométricas: puntos, líneas, polígonos. Todas ellas se describen en términos de sus respectivos vértices. Un vértice está caracterizado por 2 o 3 números en como flotante, las coordenadas cartesianas del vértice, (x, y) en 2D y (x, y, z) en 3D. Aunque las coordenadas cartesianas son las más comunes, en gráficos por ordenador también existe el sistema coordenado homogéneo en el que cada punto se describe con 4 números en coma flotante (x, y, z, w). Volveremos a él después de ver algunas nociones elementales de trazado en 3D.
Como en OpenGL todos los objetos geométricos son finalmente descritos como un conjunto ordenado de vértices.
Modelo de Representación Polígonal sobre OpenGL.
La librería gráfica OpenGL es por naturaleza una librería orientada al trabajo con modelos poliédricos,
por tanto nos será fácil realizar representación de esta naturaleza. Puntualizaremos que se trata de una
librería de funciones orientada principalmente a modelos interactivos, por ello se premia la rapidez frente
al espacio, el tipo de representación poligonal que empleara será por tanto explícita.
Las definiciones de primitivas poligonales en OpenGL se encierran entre las llamadas a las funciones:
glBegin(GLEnum tipo_primitiva) y glEnd(void). Entre dichas funciones deberemos especificar la lista
de vértices que componen nuestro polígono. La función para pasar las coordenadas de cada vértice es
glVertex3fv(GLFloat *coor), donde ‘coor’ es un vector que contiene las tres coordenadas del vértice.
Los valores normales para el tipo de primitiva son las constantes:
Valor de la Cte GL Tipo de Primitiva Poligonal
GL_POINTS Puntos aislados
GL_LINES Líneas de dos vértices
GL_LINE_STRIP Línea de cualquier numero de vértices
GL_LINE_LOOP Línea Cerrada.
GL_POLYGON Polígono de Cualquier tipo
GL_TRIANGLES Polígonos de tres lados
GL_TRIANGLE_STRIP Tira de Triangulos
GL_QUADS Polígonos de cuatro vertices
GL_QUAD_STRIP Tira de Cuadrilateros.
GL_TRIANGLE_FAN Abanico de triangulos.
Fuentes
2.-Polígono
3.-Polígonos I
2.3 Transformación bidimencional
Transformaciones Geométricas Básicas.
En este apartado veremos las operaciones de transformación que se pueden aplicar a objetos para reubicarlos o dar es un tamaño diferente.
Estas operaciones también son usadas en la visualización de rutinas que convierten una descripción de un sistema de coordenadas universales en un despliegue para un dispositivo de salida. Además, son usados en variedad de otras aplicaciones, tales como diseño de ayuda y animación por computador. Las operaciones que se aplican a descripciones geométricas de un objeto para cambiar su posición, orientación o tamaño se llaman transformaciones geométricas entre otras.
Traslación
Reposiciona un objeto desplazándolo a las nuevas coordenadas, en otras palabras, una traslación se aplica a un objeto para reposicionarlo a lo largo de una línea recta, desde una ubicación de coordenadas a otra.
Representándola en forma cartesiana.
P = (x, y) P'= (x', y')
T = (tx, ty) "El par (t subindice x, t subindice y) se llama vector de traslación"
Representándola en forma matricial.
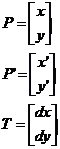
Esto nos permite escribir las ecuaciones de traslación bidimensionales en forma de matriz
para obtener: P'= P +T
Al trasladar cualquier objeto dentro del mundo virtual se debe considerar lo siguientes puntos:
• Es una transformación rígida, el objeto no se deforma
• Para trasladar líneas rectas trasladamos sólo sus extremos
• Para trasladar polígonos, trasladamos sólo sus vértices y redibujamos.
Reflexión
Una transformación que produce la imagen de un objeto en un espejo se llama reflexión. Para una reflexión bidimensional, esta imagen se genera respecto a un eje de reflexión rotando el objeto 180° sobre dicho eje de reflexión.
Esto se puede conseguir con una rotación en 180º, alrededor del eje x ó en el eje y.
Escalación
La transformación de la escalación altera el tamaño del objeto, esto lo hace escalando
cada uno de sus coordenadas con respecto al origen del eje de coordenadas
Definiendo las coordenadas
x′= x*Sx y′= y*Sy
Sx es la escala en la dirección en x y Sy es la escala en la dirección en y.
donde los parámetros de escalación Sx y Sy se asignan cualesquiera valores positivos.
Los parámetros Sx y Sy escalan un objeto en las direcciones x e y respectivamente.
Se puede escalar un objeto en otra dirección, rotando el objeto y alineándolo con el sistema de coordenadas y luego rotándolo en sentido inverso.
Descrito en la siguiente imagen con su respectiva ecuación:
Al escalar cualquier objeto dentro del mundo virtual se debe considerar lo siguientes puntos:
• Si el origen de coordenadas no se encuentra en el interior del objeto, se produce un desplazamiento
Para evitarlo, se usa un punto fijo, y se escala a partir de él. El punto fijo podría ser el centro del objeto, o uno de sus vértices, o también un punto arbitrario.
• Para escalar líneas rectas escalamos sólo sus extremos• Para escalar polígonos, escalamos sólo sus vértices y redibujamos.
Rotación
En rotación, la orientación de ésta puede ser especificada en una variedad de formas, lo que se
explica a continuación es la rotación de un punto con respecto a los ejes fijos. Un eje de
rotación define el polo sobre el cual se va a rotar, como los polos Norte y Sur de la Tierra.
x = r cos teta
y = r sen teta
Rotación alrededor de un punto
Para hacer una rotación general, podemos hacerlo mediante una composición de
transformaciones básicas.
Valores positivos del ángulo de rotación definen una rotación en contra de las agujas del reloj y lo contrario para un ángulo negativo.
En representacion matricial:
P′= R*P
Fuentes
1.-Transformaciones Geometricas
2.-TEMA 3: Transformaciones 2D
3.-CAPÍTULO III: TRANSFORMACIONES GEOMÉTRICAS
4.-CAPITULO 1 Transformaciones Geométricas en dos dimensiones
5.-CAPÍTULO 2 – Modelado y Transformaciones Geométricas
2.4 Representación matricial
Coordenadas homogéneas y representación matricial
El uso de coordenadas homogéneas permite tratar todas las transformaciones geométricas como una multiplicación de matrices.
Las coordenadas agregan un tercer componente a las coordenadas bidimensionales.
De tal forma que, un punto (x,y) pasa a ser (x,y,W). El valor de W es generalmente 1.
Coordenadas homogéneas y representación matricial
El uso de coordenadas homogéneas permite tratar todas
las transformaciones geométricas como una multiplicación de matrices.
Las coordenadas agregan un tercer componente a las coordenadas bidimensionales. De tal forma que, un
punto (x,y) pasa a ser (x,y,W). El valor de W es generalmente 1.
Representación matricial.
En el área de la graficación por computadora, es común encontrar la representación de las ecuaciones de transformación por medio de matrices, y se pueden encontrar dos tipos de notaciones para representarlas:
1.- Repesentando las coordenadas de un punto p como vectores renglón (en este caso una matriz de transformación M en 2 dimensiones, multiplica al punto por la derecha para obtener el nuevo punto p'.
p= [x1 x2], p'=[x1 x2]= p*M
2.- Representando las coordenadas de un punto p como vectores columna, en este caso una matriz de transformación M, multiplica al punto por la izquierda para obtener el nuevo punto p'.
x1 x1'
p=[ x2 ], p'=[ x2' ] =M*p
Muchas aplicaciones incluyen secuencias de transformaciones geométricas:
– Una animación requiere que los objetos se trasladen y roten en cada fotograma
– Un diseño CAD requiere muchas transformaciones hasta obtener el resultado final
• Debemos formular de forma muy eficiente toda la secuencia de transformaciones, cada transformación puede representarse como P’ = P M1+ M2
La matriz M1 contiene la información de ángulos y factores de escala
La matriz M2 contiene los términos de traslación asociados al punto fijo y al centro de rotación
Para producir una secuencia de transformaciones hay que calcular las nuevas
coordenadas en cada transformación!
P’’ = P’ M3+ M4= … = P M1M3+ M2 M3+ M4
Buscamos una solución más eficiente que permita combinar las transformaciones para
obtener directamente las coordenadas finales a partir de las iniciales
Coordenadas homogéneas
El uso de coordenadas homogéneas permite tratar todas las transformaciones geométricas como una multiplicación de matrices pues no todas las transformaciones son aplicadas a un punto como una multiplicación de factores.
Fuentes
1.-TEMA 3: Transformaciones 2D
2.-REPRESENTACION MATRICIAL DE TRANSFORMACIONES TRIDIMENCIONALES
3.-capitulo3: Transformaciónes geometricas
4.-Transformaciones geometricas
5.-Transformaciones geométricas. Introducción a la computación gráfica
El uso de coordenadas homogéneas permite tratar todas las transformaciones geométricas como una multiplicación de matrices.
Las coordenadas agregan un tercer componente a las coordenadas bidimensionales.
De tal forma que, un punto (x,y) pasa a ser (x,y,W). El valor de W es generalmente 1.
Coordenadas homogéneas y representación matricial
El uso de coordenadas homogéneas permite tratar todas
las transformaciones geométricas como una multiplicación de matrices.
Las coordenadas agregan un tercer componente a las coordenadas bidimensionales. De tal forma que, un
punto (x,y) pasa a ser (x,y,W). El valor de W es generalmente 1.
Representación matricial.
En el área de la graficación por computadora, es común encontrar la representación de las ecuaciones de transformación por medio de matrices, y se pueden encontrar dos tipos de notaciones para representarlas:
1.- Repesentando las coordenadas de un punto p como vectores renglón (en este caso una matriz de transformación M en 2 dimensiones, multiplica al punto por la derecha para obtener el nuevo punto p'.
p= [x1 x2], p'=[x1 x2]= p*M
2.- Representando las coordenadas de un punto p como vectores columna, en este caso una matriz de transformación M, multiplica al punto por la izquierda para obtener el nuevo punto p'.
x1 x1'
p=[ x2 ], p'=[ x2' ] =M*p
Muchas aplicaciones incluyen secuencias de transformaciones geométricas:
– Una animación requiere que los objetos se trasladen y roten en cada fotograma
– Un diseño CAD requiere muchas transformaciones hasta obtener el resultado final
• Debemos formular de forma muy eficiente toda la secuencia de transformaciones, cada transformación puede representarse como P’ = P M1+ M2
La matriz M1 contiene la información de ángulos y factores de escala
La matriz M2 contiene los términos de traslación asociados al punto fijo y al centro de rotación
Para producir una secuencia de transformaciones hay que calcular las nuevas
coordenadas en cada transformación!
P’’ = P’ M3+ M4= … = P M1M3+ M2 M3+ M4
Buscamos una solución más eficiente que permita combinar las transformaciones para
obtener directamente las coordenadas finales a partir de las iniciales
Coordenadas homogéneas
El uso de coordenadas homogéneas permite tratar todas las transformaciones geométricas como una multiplicación de matrices pues no todas las transformaciones son aplicadas a un punto como una multiplicación de factores.
Fuentes
1.-TEMA 3: Transformaciones 2D
2.-REPRESENTACION MATRICIAL DE TRANSFORMACIONES TRIDIMENCIONALES
3.-capitulo3: Transformaciónes geometricas
4.-Transformaciones geometricas
5.-Transformaciones geométricas. Introducción a la computación gráfica
2.5 Ventana y puerto de visión
Las transformaciones ventana-puerto de visión.
Transformación a la ventana de visión.
Mapean puntos en el mundo real a puntos en la pantalla es la manera en que van a realizar nuestros trazos y dibujos en la pantalla, pues como hemos observado en anteriores ocaciones el despliegue se hace tomando como referencia la esquina superior izquierda de nuestro monitor o pantalla donde se muestra el gráfico.
Transformación a la ventana de visión
La escena se almacenan según un sistema de coordenadas reales (metros, cm, pulgadas), el usuario verá en cada momento una subárea de la escena, o varias simultáneamente,cada subárea se mapeará en zonas distintas de la pantalla
La pantalla viene definida por un sistema de coordenadas enteras (pixels)
Proyección ortogonal.
Es cuadrada en todas sus caras. Esto produce una proyección paralela, útil para aplicaciones de tipo CAD o dibujos arquitectónicos, o también para tomar medidas, ya que las dimensiones de lo que representan no se ven alteradas por la proyección.
Una aproximación menos técnica pero mas comprensible de esta proyección es imaginar que se tiene un objeto fabricado con un material deformable, y se aplasta literalmente como una pared. Se obtendría el mismo objeto, pero plano, liso. Pues eso es lo que se vería por pantalla.
Por ejemplo, la siguiente ilustración es un render de un coche con proyección ortográfica, visto desde delante.
Proyección en perspectiva.
Reduce y estirar los objetos más alejados del observador. Es importante saber que las medidas de la proyección de un objeto no tienen por qué coincidir con las del objeto real, ya que han sido deformadas.
El volumen de visualización creado por una perspectiva se llama frustum. Un frustum es una sección piramidal, vista desde la parte afilada hasta la base
CONCEPTOS DE COLOCACIÓN DE VENTANAS
Un área rectangular que se especifica en coordenadas mundiales se denomina ventana. El área rectangular en el dispositivo de despliegue en el cual se coloca la ventana se llama puerta de visión
Los límites de la ventana se especifican en coordenadas mundiales. Las coordenadas de dispositivo normalizadas se usan con mayor frecuencia para la especificación de la puerta visión, aunque las coordenadas del dispositivo pueden emplearse si hay solamente un dispositivo de salida en el sistemas. Cuando se usan coordenadas de dispositivo normalizadas, el programador considera el dispositivo de salida como aquel que tiene valores coordenados dentro del intervalo de 0 a 1.
Fuentes:
1.-TEMA 3: Transformaciones 2D
2.-Tema 4. Proyecciones y viewport
3.-PUERTO DE VISION, PROYECCION ORTOGONAL Y DE PERSPECTIVAS
1.-TEMA 3: Transformaciones 2D
2.-Tema 4. Proyecciones y viewport
3.-PUERTO DE VISION, PROYECCION ORTOGONAL Y DE PERSPECTIVAS
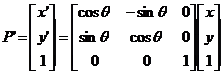
No hay comentarios.:
Publicar un comentario