Unidad 3

Unidad 3

- Representaicon de objetos en tres dimenciones
URL: http://graficacionito.blogspot.mx/2013/10/31-representaicon-de-objetos-en-tres.html 

- Visualizacion de objetos
URL: http://graficacionito.blogspot.mx/2013/10/32-visualizacion-de-objetos.html 

- Transformaciones tridimencionales
URL: http://graficacionito.blogspot.mx/2013/10/33-transformaciones-tridimencionales.html

- Lineas y superficies curvas
URL: http://graficacionito.blogspot.mx/2013/10/34-lineas-y-superficies-curvas.html 



Conclusión:
La Graficación en 3 dimensiones nos ha dado una gran capacidad para plasmar ideas que necesitamos mostrar o comprobar, desde luego nos permite simular alguna idea, si ésta parece inusual o bastante fuera de la realidad pero en si, ese es su objetivo.
Entendí los pasos para la creación de elementos gráficos consta de 4 complejos pasos:
Modelado, Iluminación, Animación (si es que se necesita) y Renderizado.
Todo esto depende mucho en la manera que se han representado visualmente, pues existen muchas maneras de mostrar un grafico, mencionando algunas como los modelos alámbricos, de superficies y solidos.
A grandes rasgos entendemos que los gráficos pueden ser mostrados desde muchas perspectivas y vistas, que facilitan su creación, entendimiento o su demostración.
Las existencia de diferentes vistas en el medio de Graficación, nos da una idea de lo detallista que se debe hacer al crear algún diseño, por mencionar alguno; la proyección cónica, siendo la mas usual y general al presentar un grafico, nos muestra un punto de observación y el objeto, donde se encuentran relativamente cercanos.
Cabe mencionar que todos los gráficos por computadora que han existido, hay requerido de algún modelo matemático o cálculos vitales para su construcción. Y no es la excepción en la actualidad, pues con las transformaciones tridimensionales se utilizan matrices de transformación donde se expresan y se resuelven posiciones en coordenadas homogéneas, que nos permite representar todas las ecuaciones de trasformación geométrica (como la multiplicación de una matriz).


Se puede mencionar unos puntos adicionales sobre la graficacion en 3D:

• Técnicas muy variadas para el modelado de objetos 3D
• Multitud de herramientas profesionales y amateurs para modelado y desarrollo de objetos 3D
• Gran capacidad de representación e infinitas posibilidades

3.1 Representaicon de objetos en tres dimenciones

Anteriormente de la existencia de la computacion grafica,  los objetos tridimensionales se han representado en dos dimensiones,  desde luego se consideraba muy firme el aspecto matematico  siguiendo las normas de la perspectiva para conseguir una representación que parezca lo más aproximada posible a la realidad o a una idea concebida en la mente de algun creador, o mediante diversas vistas correspondientes a la proyección del objeto sobre diferentes planos, acompañadas de cotas, secciones, vistas de detalle, etc. que permitan reproducir exactamente el objeto dibujado.

 

 

 

 

 

Se llaman gráficos 3D  (escrito de una manera simplificada)   a todos los objetos que se pueden dibujar en un espacio R3 (3 dimenciones): puntos, segmentos, curvas, superficies y varios cuerpos formados por caras poligonales, así como textos y macros.

Existen varias razones para querer representar un objeto mediante un modelo de superficie:

 

•Cuando el objeto mismo es una superficie que podemos suponer sin grosor (por ejemplo, chapa metálica del capó de un vehículo). Este tipo de representación nos permite visualizar
superficies abiertas, mientras que los sólidos se caracterizarán por tener su superficie
necesariamente cerrada sobre sí misma.
•Cuando tan sólo nos interesa visualizar su aspecto visual externo, sin detalles sobre su estructura interna, aunque el objeto ocupe un cierto volumen.
•Cuando deseamos realizar una visualización en tiempo real, y para ello utilizamos hardware o
software gráfico que está sólo preparado para visualizar polígonos.



Basicamente podemos representar los objetos graficos en tres dimenciones en las siguientes  vistas.

•Modelos alámbricos
Muestra los objetos utilizando líneas y curvas para representar los contornos.
Sólo contienen elementos que materializan aristas de objeto. Muy rápidos para prototipado.

Nótese que en este diseño, solo se puede visualizar los trazos, mas nunca un objeto con-ciso y solido pues el objetivo de esta vista básicamente es demostrativo  pero con la cualidad de mostrar la composicion tanto interna como externa, es decir, una radiografia al objeto.









• Modelo de superficies
Definen caras de objeto mediante superficies (3 ó 4 lados). Permiten representar superficies curvas con un grado de  complejidad.

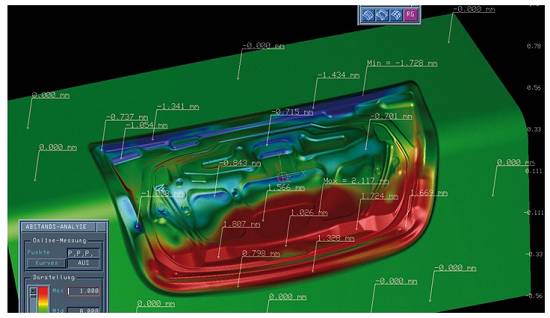
Ahora el objeto se puede apreciar mejor pues se muestra las superficies que lo delimitan. Esta vista es demostrativa a lo que puede llegar a ser cuando el diseño esté terminado ó una vista informal del objeto pues aun no es posible gozar una apreciación completa.







•Modelo de sólidos
Representan todo el volumen de un objeto,permite análisis de propiedades físicas, creación mediante primitivas (esfera, cono, etc.), operaciones (extrusión, revolución,etc).

Ahora el objeto goza de una apreciacion completa,  pues con esta vista, casi podemos visualizar el diseño construido en la  vida real.
Esta vista se caracteriza por mostrar un trabajo final al diseño, despues de haber depurado detalles y agregando otros para dar la mayor impresion de realismo.









 Fases para la creación de elementos o gráficos tridimensionales.





Modelado: La etapa de modelado consiste en ir dando forma a objetos individuales que luego serán usados en la escena 

Iluminación: Creación de luces de diversos tipos puntuales, direccionales en área o volumen,   con distinto color o propiedades. Esto es la clave de una animación.









Animación: La animación es un proceso utilizado para dar la sensación de movimiento a imágenes o dibujos o a otro tipo de objetos inanimados. Se considera normalmente una ilusión óptica.









Renderizado: Se llama renderización al proceso final de generar la imagen 2D o animación a partir de la escena creada. Esto puede ser comparado a tomar una foto o en el caso de la animación, a filmar una escena de la vida real. El software de rénder puede simular efectos cinematográficos como el lens flare, la profundidad de campo, o el motion blur (desenfoque de movimiento).

3.2 Visualizacion de objetos

En este caso trataremos con las proyecciones que van del espacio al plano (3D a 2D). La proyección de objetos tridimensionales serán definidos por la intersección de líneas rectas que van desde un 
centro de proyección u ojo, hasta cada punto del objeto.

Proyección Acotada

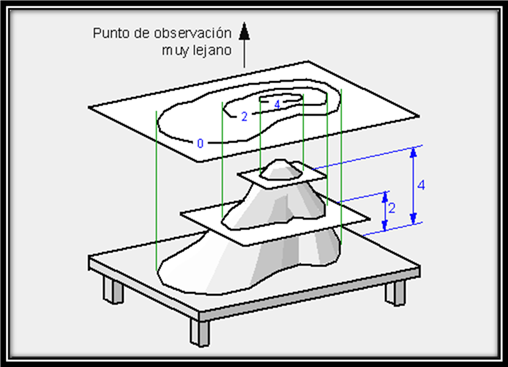
Es una proyección ortogonal sobre la que se acotan en cada punto, línea, u objeto representado la altura (cota) del mismo con respecto a cualquier plano de referencia que sea paralelo al plano de proyección. La proyección acotada es muy práctica cuando es necesario representar gráficamente objetos irregulares; razón por la cual se usa frecuentemente para el diseño de techos de viviendas; construcción de puentes, represas, acueductos, gasoductos, carreteras, determinación de áreas de parcelas, trazado de linderos, y dibujos topográficos de plantas y perfiles de terrenos, entre otros.


Proyección Cónica.

Denominada también perspectiva. Se obtiene cuando el punto de observación y el objeto se encuentran relativamente cercanos. Es el sistema de representación gráfico en donde el haz de rayos proyectantes confluye en un punto (el ojo del observador), proyectándose la imagen en un plano auxiliar situado entre el objeto a representar y el punto de vista.

Geométricamente, una fotografía es una perspectiva; razón por la cual la proyección cónica sobrepasa en excelencia a los demás sistemas de proyección por ser la que más se acerca a la vista real obtenida por el observador.


Proyección Cilíndrica

Se obtiene cuando el punto de observación se encuentra a una distancia tan grande del objeto, que permita considerar que las proyectantes son paralelas al interceptarse con el plano de proyección. Los principales tipos de proyección cilíndrica son:

• Proyección Ortogonal

 

También denominada proyección ortográfica. Se obtiene cuando las proyectantes son perpendiculares al plano de proyección. La proyección ortogonal es muy utilizada en el diseño de piezas mecánicas y maquinarias.

 

La proyección ortogonal es el método que se utiliza para representar la forma exacta de un modelo por medio de dos o más vistas sobre planos que forman ángulos rectos entre sí. La proyección se obtiene por la intersección de las perpendiculares trazadas desde el modelo sobre los planos de proyección.

 

• Proyección Oblicua

 

Se obtiene cuando las proyectantes no son perpendiculares al plano de proyección. Preferentemente al dibujar en proyección oblicua se coloca el plano de proyección paralelo a una de las caras principales del objeto; ya que de esta forma dicha cara se proyectará en verdadero tamaño.

3.3 transformaciones tridimencionales

Las transformaciones de los objetos, son la Posición, la Rotación y la Escala.

Determinan la ubicación en el la escena mediante coordenadas trigonométricas en los ejes de coordenadas  x, y y z. Se refieren a todo el objeto.  La manera más fácil de conseguir las transformaciones básicas (traslación, rotación, escalación, en general las transformaciones afines) es utilizando matrices de transformación.


Coordenadas homogéneas
Nos será útil sustituír las coordenadas (x, y) por las coordenadas (xh, yh, h), llamadas coordenadas homogéneas, donde:
x = xh/h,    y = yh/h

(xh, yh, h) = (h . x, h . y, h)

Expresar posiciones en coordenadas homogéneas nos permite representar todas las ecuaciones de transformación geométrica como multiplicaciones de matriz. Se representan las coordenadas con vectores de columna de 3 elementos y las operaciones de transformación se expresan como matrices de 3 por 3. 


Matrices de transformación en 3D más comunes
Traslación
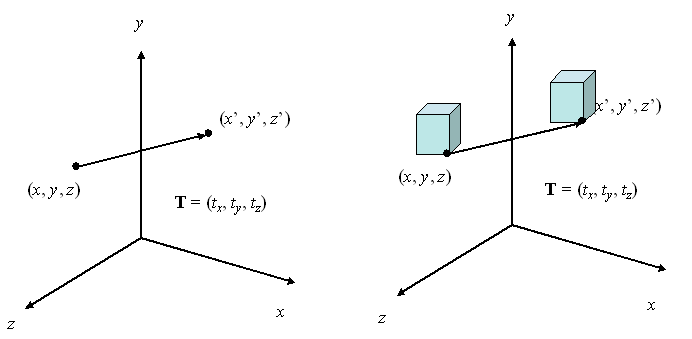
En la representación homogénea tridimensional de las coordenadas, se traslada un punto de la posición P = (x, y, z) a la posición P’ = (x’, y’, z’) con la operación de matriz
P’ = T x P

donde P y P’ son vectores columna como matrices, la matriz

T=1 0 0 tx
     0 1 0 ty
     0 0 1 tz
     0 0 0 1
y tx, ty y tz especifican las distancias de traslación en x, y y z

x’ = x + tx
y’ = y + ty
z’ = z + tz

Rotación

Para generar una transformación de rotación, debemos designar un eje de rotación respecto del cual girará el objeto, y la cantidad de rotación angular, es decir, un ángulo (θ).

Una rotación tridimensional se puede especificar alrededor de cualquier línea en el espacio.

Los ejes de rotación más fáciles de manejar son aquellos paralelos a los ejes de coordenadas.

Se forma una matriz de rotación inversa al sustituír el ángulo de rotación θ por –θ. Los valores negativos para los ángulos de rotación generan rotaciones en una dirección en el sentido del reloj, de modo que se produce la matriz identidad cuando se multiplica cualquier matriz de rotación por su inverso

Escalación
La matriz para la transformación de escalación de una posición P = (x, y, z) con respecto del origen de las coordenadas se puede escribir como:

       |ex  0  0  0 |
       |0  ey  0  0 |
       |0   0  ez 0 |
 S= |0   0  0  1 |

Donde ex, ey, y ez pueden tener cualquier valor positivo (valores de escalación en cada uno de los ejes, si estos no son iguales, se cambian las dimensiones relativas en el objeto).
La escalación con respecto a una posición fija seleccionada se puede obtener con la siguiente secuencia de transformación:

1. Se traslada el punto fijo al origen.
2. Se escala el objeto con respecto al origen.
3. Se traslada el punto fijo a su posición original.

3.4 lineas y superficies curvas

La necesidad de representar curvas y superficies proviene de modelar y representar objetos reales o ficticios.
Normalmente no existe un modelo matemático previo del objeto, y el objeto se aproxima con “pedazos” de planos, esferas y otras formas simples de modelar cercanos a los correspondientes puntos del objeto.

Definiciones Básicas
Una curva es  una línea continua de una dimensión, que varía de dirección paulatinamente.

Una superficie es una extensión en que se consideran sólo dos dimensiones.


SUPERFICIES CURVAS

Las superficies curvas pueden generarse a partir de un conjunto funciones matemáticas que definen la superficies o bien a partir de un conjunto de puntos de datos especificados por el usuario.
Cuando se especifican funciones de curvas, un paquete puede emplear las ecuaciones definidoras para localizar y gráfica posiciones de pixeles a lo largo de la trayectoria de la curva, casi igual como sucede con las curvas en dos dimensiones.

La definición analítica de una dada curva puede hacerse de varios modos y se relaciona directamente con la forma de representarla gráficamente:

• Explícitamente :

 y = f(x)

• Implícitamente:

  f(x, y) = 0

• Paramétricamente:

   x = x(t)
   y = y(t)

Representación Explícita
Es la mas conocida desde que nos ensenaron a utilizar las coordenadas cartesianas para graficar funciones.
En 3D, para representar una curva se requieren dos ecuaciones:
y = f (x),  z = g(x)
Obteniendo una superficie  en 3D que será:
z = f (x, y)


Representación Implícita
Para curvas y superficies estándar (rectas, círculos, planos, toroides, etc.), este tipo de definición es mas directa y permite visualizar y modificar sencillamente parámetros importantes y específicos de cada curva (radio en un circulo, distancia al origen en un plano, etc.).
En 3D, una superficie se describe por
f(x, y, z) = 0
Ejemplo
• Una esfera: x2 + y2 + z2 – r2 = 0
• Una curva corresponde a la intersección de dos superficies:
f(x, y, z) = 0 y g(x, y, z) = 0
Nota: el punto (x, y, z) debe pertenecer a ambas superficies.

Representación Paramétrica
El valor de cada variable espacial se expresa en términos de una variable independiente (t), llamada parámetro.
Estas funciones juntas han de  formar las ecuaciones paramétricas de una curva:
x = x(t)
y = y(t)
z = z(t)
Cada valor de t determina un punto (x,y) que se puede representar en un sistema de coordenadas.
Superficie Paramétrica al conjunto de puntos (x,y,z,) dados por r(u,v)= x(u,v)i + y(u,v)j + z(u,v)k.
Las Ecuaciones x=(u,v), y=(u,v) y z=(u,v) se llaman Ecuaciones Paramétricas de la superficie.


La configuración de los objetos gráficos 3D curvas y superficies también se puede ilustrar con mayor detalle mediante la siguiente escena:

Variables para la escala y los giros
En gráficos 3D se agregaron unas variables para conocer y controlar los ángulos de giro del espacio : <Espacio>.rot.y y <Espacio>.rot.y donde <Espacio> es el nombre del espacio.

También se agregaron las variables <Espacio>.escala y <Espacio>.observador que sirven para controlar la escala y la distancia aparente al observador, ambas se miden en pixeles. La siguiente escena ilustra explícitamente el uso de estas variables. Observe que si el usuario cambia la escala o gira el espacio arrastrando el ratón, los controles numéricos se actualizan con los nuevos valores de la escala y las rotaciones.

pero . . .

¿Cómo se dibujan las curvas o superficies en la pantalla de la computadora?

Aproximando esta curva con una poligonal.
Así encontramos los puntos que serán mostrados. Y los puntos serán unidos a través de líneas.

Esta forma es totalmente diferente pues la curva o superficie es el resultado de un procedimiento o algoritmo; en general modificando una curva o  superficie simple de partida.
Ej.: Dividir en tres cada tramo de una poligonal y reemplazar los dos tramos que convergen a un vértice original por el que une los dos nuevos vértices cercanos al original: